WILLIAM STANLEY JEVONS: EL USO DE LAS PROBABILIDADES Y EL CÁLCULO*
JOHN JAMES MORA R.
Economista Universidad del Valle. Maestría en Economía Ambiental Universidad Autónoma de Madrid. Jefe del Departamento de Economía de la Universidad Icesi e-mail:jjmora@icesi.edu.co
*Este ensayo comenzó a escribirse hace casi cinco años, cuando era asistente de investigación del profesor Boris Salazar en la Universidad del Valle. Muchos eventos impidieron culminar esta "deuda intelectual" que tenía con Boris, quien nunca ha reparado en brindarme su desinteresada crítica y, de quien siempre estaré en deuda.
RESUMEN
En el capítulo tercero de la TPE, Jevons recurre al uso de las probabilidades como un método alternativo para analizar el intercambio de las mercancías. Jevons, decide no continuar con el uso de las probabilidades en los capítulos siguientes; su teoría se bifurca imperando el uso del cálculo diferencial. La explicación de esta bifurcación radica en la existencia de dos métodos alternativos para explicar el análisis del intercambio: La teoría de las probabilidades y el cálculo diferencial. Usar el cálculo diferencial no significaba que fuese el método más eficiente, pues no sólo existieron errores al maximizar como muestra Westergaard (1874), sino también problemas metodológicos, como muestran Stigler (1956) y Blaug (1985). Por otro lado, el método de las probabilidades habría significado para el análisis del intercambio, un problema de valores esperados y un camino totalmente diferente para la revolución marginalista.
Palabras claves: Historia de la economía, Teoría de la utilidad.
JEL classification: A11, B1, B41.
INTRODUCCION
En el año de 1871 aparece la primera publicación de Theory of Political Economy2 de W.S. Jevons, que junto a la publicación de Leon Walras y Francis Edgeworth, fueron eventos conocidos posteriormente como la Revolución marginalista (Schumpeter (1954), Blaug (1985), Black et al (1979)). La simultaneidad entre las obras de Jevons y Walras ha sido tratada por Schumpeter (1954), Mirowski (1989) e Ingrao e Israelsen (1990) entre otros, siendo este evento un capítulo en la historia económica, que tal vez habría sido diferente si en lugar de utilizar el análisis marginal Jevons hubiese usado las probabilidades que estaban a su alcance por su relación con De Morgan y Boole.
Este artículo discute en primer lugar, hasta dónde, con las herramientas de la época, se podría explicar la utilidad usando probabilidades. Y, en segundo lugar hasta dónde Jevons usó las probabilidades y qué tan acertado fue en escoger el cálculo para solucionar el problema de la utilidad e intercambio como método alternativo a las probabilidades.
JEVONS Y EL USO DE LA LOGICA
Después de su estadía en Australia,3 Jevons regresa a University College (Londres) complementando su Master of Arts en 1842. Durante los años sesenta Jevons vive un período de prolífico pensamiento y, es en éste cuando gracias a su primo H. Enfield Roscoe, que Jevons se acerca al círculo académico y produce dos obras "Pure logic, or the logic of quality apart from quantity" en 1863 y "Brief account of a general mathematical theory of political economy" en 1866. Durante este período se da un rápido desarrollo en la lógica simbólica por George Boole y Augustus de Morgan (Black, 1982). Jevons, por su parte, también realizará contribuciones al pensamiento inglés,4 una de las más recordadas es su famosa "Machina Logic",5 que a partir del principio de sustitución de similares, se constituye en pionera de las modernas computadoras (Black, 1988).
Hacia 1874, Jevons publica "The Principles of Science"6 formalizando su método lógico. Los trabajos sobre lógica le permitirán a Jevons madurar la idea, de que al igual que las ciencias naturales, la economía podía ser tratada como una ciencia formal "la cual además de ser lógica es también matemática" (Jevons TPE, 1871,78) y, por lo tanto, que no requería de una construcción específica como ciencia social. El desarrollo de la lógica va a permitirle a Jevons mantener un "Principio unificador" en la economía, de tal forma que su creencia de que la economía estaba dentro de la jerarquía de las ciencias, justificaba "un cálculo de los efectos morales, una clase de investigación astronómica física de las perturbaciones mutuas de los individuos" (TPE).7 El punto de partida consistió entonces en elegir aquella rama del conocimiento, que le permitiera tratar los sentidos de igual forma que las cantidades "Nosotros siempre tratamos los sentimientos como capaces de ser más o menos, y yo ahora sostengo que ellos son cantidades capaces de ser tratadas científicamente" (1866, pág.9), de tal forma que existiera una clara ruptura con el método imperante de la época: la aproximación de Cliffe Leslie con la metodología de la escuela histórica alemana y, el método abstracto - deductivo de Ricardo y Mill que a la vez combinaba una concepción interpretativa de la "naturaleza humana" (Ellen 1979, pág. 269).
Primera hipótesis: A partir del uso de la lógica, el paso siguiente para tratar la utilidad eran las probabilidades, este camino fue trazado por Boole.
George Boole (1854), al igual que Jevons, se fundamenta en Senior "La riqueza consiste en las cosas transferibles, limitadas en cuanto a la oferta y, o bien productoras de placer o preventivas del dolor" (pág. 96). Si w es la riqueza, s las cosas limitadas en la oferta, t las cosas transferibles, p las productoras de placer y, r las que previenen el dolor, Boole llega a las siguientes ecuaciones:
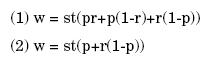
Como señala Boole(pág.97) a partir de la ecuación anterior se puede eliminar cualquier término que no se desee tener en cuenta y, expresar el resultado por solución y desarrollo. Considerando la expresión para la riqueza utiliza el sistema lógico como indicativo de eliminación de términos medios, para esto, toma a r como término a eliminar. Si se hace r= 1, el primer miembro se convierte en w - st y si se hace r= 0 entonces se convierte en w - stp. De donde:
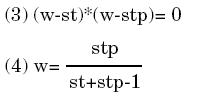
Y, desarrollando la ecuación obtenemos:
Lo cual significa que la riqueza consiste en todas las cosas limitadas en la oferta, transferibles y productoras de placer y, un indefinido remanente de cosas limitadas en las ofertas transferibles y, no productoras de placer. El uso que hace Boole de la lógica8 como método para explicar la riqueza en relación con las cosas que producen placer, es diferente al aplicado por Jevons. En el análisis realizado por Boole, sólo se necesita saber las cosas que producen placer o no placer, así se elimina el término r. De esta forma, como lo expresa Boole, la lógica posee dos clases de relaciones: relaciones entre cosas y relaciones entre hechos. Sin embargo, ya que los hechos son expresados por proposiciones, las relaciones podrían ser resueltas dentro de una relación entre proposiciones. Así, Boole muestra cómo la forma de expresar la utilidad no es exclusiva en términos de aumentos o decrecimientos, ya que puede ser definida en una sola dirección: posee la cualidad o no la posee.
A partir de la ecuación (5), es posible aplicar la teoría de las probabilidades para definir la riqueza en Senior, lo que indudablemente lleva a la teoría de la utilidad en Jevons. Como Boole señala, la lógica es el punto de partida de la teoría de las probabilidades: "El propósito del siguiente tratado es investigar las leyes fundamentales de aquellas operaciones en la mente mediante las cuales se lleva a cabo el razonamiento; expresarlas en el lenguaje simbólico de un cálculo, establecer sobre esta base la ciencia de la Lógica y construir su método; hacer de dicho método la base de un método general que permita la aplicación de la doctrina matemática de las probabilidades" (Boole, pág. 11) y "Como las investigaciones en que estamos a punto de entrar ahora se basan en el empleo del cálculo de la lógica, es necesario explicar ciertos términos y modos de expresión que se derivan de esta aplicación. Por el suceso X entiendo aquel suceso del cual la proposición que afirma el acontecimiento se expresa simbólicamente por la ecuación X=1" (Boole, pág. 226). Es decir, la lógica permite a través del principio de eliminación de términos llegar a las probabilidades y, a partir de la investigación de Boole sobre la riqueza en Senior es posible llegar a una teoría de la utilidad usando la teoría de las probabilidades.
JEVONS, DE MORGAN Y BOOLE
Para Black (1972) University College influenciaría el pensamiento de Jevons en dos vías, por un lado la introducción de la economía al hedonismo psicológico a través de la filosofía utilitarista de Jeremías Bentham y, por otro lado, la influencia de la lógica y el tratamiento de cantidades por Augustos de Morgan en el uso de la lógica matemática.
De Morgan es el primer profesor de matemática de University College, a la edad de 22 años y, sus contribuciones a las relaciones entre las matemáticas y la lógica permiten situarlo junto con Boole entre los mejores de Inglaterra (D.E, Smith 1951, Black 1972).
Jevons toma clases con De Morgan como "Lower Junior" y después como "Higher Junior". Las clases con De Morgan le permiten pensar a Jevons la utilidad como un concepto susceptible de tratamiento estadístico según Hicks y, es en los años de "Higher Junior", entre 1852 y 1853, que De Morgan introduce en sus cursos los conceptos elementales sobre las probabilidades (Black 1972). Este también es el inicio de Jevons en una nueva forma de tratar las relaciones entre los individuos, pero que no se reflejará en "Brief account of a general mathematical theory of political economy" , sino en la TPE: "Antes de la época de Pascal, ¿quién hubiera pensado en medir la duda y la creencia? ¿Quién podría haber concebido que la investigación de los juegos pequeños de oportunidad habría de llevar a la creación de tal vez la más sublime rama de la ciencia matemática: la teoría de las probabilidades?" (TPE, pág. 8).
Entre Brief Account y la TPE, madura Jevons sus ideas sobre las probabilidades, pero también es un período en el cual se evidencia un gran dilema en su obra:
No cabe duda de que el avance en probabilidades realizado por Boole, era un buen punto de partida para Jevons, aun cuando la mayoría de las ciencias estaban en formación. Cournot es un buen ejemplo de la incertidumbre reinante en la época, en torno al uso de las probabilidades, pues éste no creía en el uso de la estadística como algo científico (White 1989) y entonces ¿cómo desarrollar una teoría del intercambio en un método que apenas se estaba desarrollando? La economía, una ciencia que comparada a las demás era menor ¿requería de una construcción específica?
Si las probabilidades constituían el método que le permitiría analizar los deseos humanos, que de hecho, como pensaba Jevons, son "el grado final de la utilidad que es la función sobre la cual la teoría económica podría ser fundamentada" (TPE, 5 edición, pág. 52) entonces ¿por qué Jevons cambió el método de las probabilidades, por el uso del cálculo diferencial en el capítulo cuarto? Lo que significa asumir un esquema de utilidad fija donde las probabilidades de las causas accidentales o fortuitas se anularían9 y, entonces, el grado de utilidad sería "en lenguaje matemático, el coeficiente diferencial de μ considerado como una función de X," (TPE, 5).
Suponer que Jevons requiriese de un contexto específico, esto es, que no pudo encontrar un lenguaje económico que se adaptara a la teoría de las probabilidades, es falso, en tanto para Jevons las probabilidades no se diferencian, como método, del cálculo, por lo cual no había necesidad de buscar un contexto específico.
Sin embargo, la relación que el capítulo tercero guarda con toda la TPE, es un interrogante que ha llevado a Kriström (1990) a suponer que en el capítulo tercero, más específicamente la sección 2 "Distribución de la mercancía en el tiempo" (pág. 71-74), existe la posibilidad de que Jevons introdujera un concepto, cuya analogía moderna sería "option price" en términos de Weisbrod´s, para diferenciar la existencia de una mercancía en el futuro: "Within modern economic terminology it is possible that both Jevon´s and Weisbrod´s ideas are more closely related to what is know as option price (the sum of expected consumer surpluses and option value)" Kriström, pág. 86.
Las conclusiones de Kriström, están basadas en el siguiente párrafo de Jevons: "Only when there arises a degree of probability, however slight, that a particular object will be needed, does it acquire prospective utility, capable of rendering it desirable possession" (TPE, pág.70).
La idea de Kriström es interesante, sin duda, pero no deja de ser una especulación, sobre las conclusiones de dicho capítulo, ya que el grado de utilidad asignado a cada mercancía, en relación con una cantidad, sólo se define en el intercambio y no ex ante, como lo indica el mismo Jevons y, entonces "como la probabilidad es menor, la mercancía asignada a cada día es menor, y así el grado de utilidad es mayor" (Jevons pág. 72).
Esto significa, siguiendo el análisis de Kriström, un valor esperado menor en el tiempo, y una diferencia en el intercambio cada vez mayor en el valor de las mercancías. Mientras para Kriström, el capítulo tercero significa un problema del valor esperado con antecedentes en Jevons, para la teoría económica podría haber sido decisivo en el análisis económico si Jevons hubiese considerado seguir bajo el naciente mundo de la estadística y las probabilidades. Jevons, como muy bien lo expresa Kriström, parte en dicho capítulo de analizar la capacidad de las cosas de ser deseables y de generar utilidad, una idea que Boole (1854) ya había analizado en la época.
Hipótesis No. 2: El uso del cálculo como método para tratar la utilidad en Jevons fue un camino irreversible que se autorreforzó.
Jevons considera que las cosas no tienen una cualidad inherente a ellas, algunas poseen utilidad y otras no. Esta cualidad resulta de las relaciones entre los placeres y los dolores. Expresado de esta forma, algunas cosas poseerán utilidad y otras no. Las condiciones según las cuales se determina el valor suponen la existencia de una ley, bajo la cual en cualquier instante del tiempo se puede determinar la utilidad de cualquier mercancía. Dicha "ley" requeriría en primer lugar de una estrategia que tuviera la elegancia de los métodos que se utilizaban en las ciencias más avanzadas de la época, como eran la física y la matemática. En segundo lugar, que fuera lo suficientemente explicativa y, en tercer lugar, que el método utilizado fuese "neutral" para no dar lugar a confusiones y, por lo tanto, posible de ser aceptado por cualquiera.
Para cumplir con estos requisitos, Jevons recurre al uso del cálculo diferencial, pues "la variación de la función expresando el grado final de la utilidad es el más importante punto de los problemas económicos" (TPE pág. 53). Una vez definida la cantidad de un bien, el problema radica en cómo determinar el grado final de utilidad.10
Para definir el grado final de utilidad, es necesario suponer que la variación de la utilidad es decreciente con respecto a las cantidades, cuando ésta es creciente "La ley general, el grado de utilidad varía con la cantidad de la mercancía, y al final decrece con las cantidades crecientes" (Jevons capítulo III), lo cual se hace suponiendo variaciones con respecto a las cantidades (ΔX). Jevons, consideró entonces que el concepto de cálculo diferencial estaba lo suficientemente explícito como para realizar explicaciones más exhaustivas sobre estas relaciones.11 Así, Jevons comienza el capítulo cuarto con la siguiente cita: "El intercambio es un proceso importante en la maximización de la utilidad y en el ahorro del trabajo, esto resulta de la necesidad de definir las condiciones con las cuales aparece el valor".12
Para Jevons este punto era más importante que tener toda una teoría sistemática del "mundo económico", donde existieran unas interrelaciones lógicas y formales como en Walras. Jevons, sin duda era más modesto, su preocupación radicaba en cómo conciliar una teoría donde el valor estuviera determinado para la tasa marginal de la utilidad con una teoría del intercambio. Así, como mencionará Jevons, el principio de la utilidad radica en poder distribuir una mercancía en varios usos y la teoría de la utilidad "da, teóricamente hablando, una solución completa a la pregunta" (TPE, pág. 59).
En el capítulo tercero, Jevons define la utilidad, no pareciendo necesitar el intercambio para definirla. El supuesto que necesariamente debiere satisfacer, como lo menciona Creedy (1980), consistirá en maximizar la utilidad de una persona sujeto a la condición de que la utilidad de la segunda persona permanezca constante (pág. 373). Y, que según Westergaard (1874) podría verse como un problema de maximización restringida:
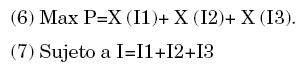
Siendo p el posible producto, X = el producto de la tierra, I = el trabajo usado en la tierra, i,j=1,2,3. I = total de trabajo disponible y dx /dI es el producto marginal del trabajo, en donde las condiciones de segundo orden son d2p 0 y la solución implica "I1+I2+I3=1" bajo rendimientos decrecientes y competencia perfecta [Logan y Yeung(1990)].13 Antes de la publicación de la segunda edición de la TPE, esta solución se la envió Westergaard a Jevons.14 Jevons aduciendo que escribía para un lector que no era un profesional en matemáticas15 rehusó utilizar las notaciones necesarias, para encontrar en una función, cuando hay un máximo o un mínimo. Esto no implica que Jevons no conociera las propiedades del cálculo diferencial16 aunque queda la duda de hasta dónde manejaba Jevons el uso de las herramientas matemáticas como lo menciona Creedy "Walras y Jevons no pudieron usar el método Lagrangiano" (Creedy 1980).
El método usado por Westergaard, para demostrar que a partir de las condiciones de primer y segundo orden, se puede encontrar la máxima utilidad17 no fue usado por Jevons en la TPE. Pero este método podría conciliar las diferencias que Stigler observaba entre el capítulo tercero y el cuarto, y que da lugar a la crítica de Stigler, para quien la respuesta de Jevons de apelar a un cuerpo comerciante y a la ley de indiferencia, es ingeniosa pero ilícita, "un cuerpo comerciante es un cuerpo de compradores y vendedores de una mercancía en un mercado competitivo y la ley de indiferencia es solamente un precio en un mercado" (Stigler, 1956, pág. 90).18
Parte de la controversia radica en que la solución de Jevons es posible, ya que como menciona Walras, Jevons utiliza cantidades, mientras que los precios son desconocidos,19 por lo tanto, la solución estará dada en términos de cantidades. Blaug (1973 pág. 425) menciona que Jevons al llegar a este punto "formula la ley de la utilidad marginal decreciente y apela a la ley fisiológica, citando a Jennings en su ayuda".20 Esta estrategia le permite suponer que en equilibrio no existen pérdidas o ganancias en la utilidad (TPE pág. 96), siendo ingenioso en esta parte: "En otras palabras si los incrementos de las mercancías intercambiadas son establecidos a una tasa, sus utilidades podrían ser iguales para ambas partes" (pág. 96), lo cual está garantizado con una función decreciente.
Sin embargo, Jevons no consigue garantizar que en el intercambio se alcance el grado final (máximo) de la utilidad21 y, como menciona Blaug "la utilidad marginal no es la derivada de la utilidad con respecto a la cantidad, sino el incremento diferencial de la utilidad" (pág. 426). En este sentido, los agentes económicos de Jevons podrían resultar engañados: la utilidad total puede bajar a medida que se va consumiendo un mayor número de unidades, a pesar de que la utilidad marginal continúe siendo positiva (Paradoja de Wieser).22 De esta forma, el grado de utilidad podría ser máximo antes del intercambio y, entonces ¿para qué realizar este?
La estrategia de usar cantidades, reivindica el uso de las matemáticas, ya que "nuestra ciencia debe ser matemática, simplemente porque entiende con cantidades" (TPE, pág. 3). Sin embargo, le impone a Jevons el método del cálculo pues para garantizar el intercambio entre los agentes deberá maximizar. No cabe duda, que la presentación del problema con respecto a sus predecesores, usando las matemáticas, muestra un claro rompimiento con la teoría clásica. Sin embargo, no seguir la vía de las probabilidades y rehusar utilizar el Lagrangiano, dejan la duda de hasta dónde su incursión en la teoría económica habría sido exitosa.
CONCLUSIÓN
En el capítulo tercero de la TPE, Jevons recurre al uso de las probabilidades como un método alternativo para analizar el intercambio de las mercancías. Sin embargo, este método es abandonado en el siguiente capítulo, eliminando la posibilidad de introducir aquellas "causas fortuitas" que pudieran modificar el valor de las mercancías. Como muestra Kriström, esta es una primera aproximación al análisis de la utilidad esperada, desde un esquema de probabilidades.
Jevons decide no continuar con el uso de las probabilidades, en los siguientes capítulos de la TPE, su teoría se bifurca imperando el uso del cálculo diferencial. La explicación de esta bifurcación radica en la existencia de dos métodos alternativos para explicar el análisis del intercambio: La teoría de las probabilidades y el cálculo diferencial. La razón de porqué el cálculo diferencial imperó sobre las probabilidades no es clara, uno podría argüir que el cálculo diferencial era más complementario con la teoría de Jennings y, por lo tanto, que reforzaba los resultados encontrados, al punto que le permitía hablar con ilimitada confianza, como observara Schumpeter (1954) "Los primeros teóricos de la utilidad hablan de los hechos psíquicos con ilimitada confianza, los consideraban elementos del acervo de la experiencia común, como salidos de esa fuente de conocimientos de la marcha de la vida cotidiana, que ninguna persona razonable puede poner en juicio" (pág. 1.150).
Haber usado cálculo diferencial no significaba que fuera el método más eficiente que pudiera utilizar Jevons, pues no sólo existieron errores al maximizar como muestra Westergaard, sino también problemas metodológicos al usar el cálculo diferencial, como lo señalan Stigler (1956) y Blaug (1985).
No cabe duda de que la suerte de Jevons fue menos afortunada que la de su compañero de "revolución marginalista" Leon Walras, pues Jevons no trascendió en la historia de la economía como sí lo hizo Walras. Esto en parte se debe a que la estrategia en torno al uso de las matemáticas fue diferente también: Mientras Walras usó los elementos brindados por Piccard(Salazar, 1996) Jevons rechazó los que le brindó Westergaard.
Finalmente, el método de las probabilidades en el intercambio hubiera representado para el análisis del intercambio un problema de valores esperados y un camino totalmente diferente para la revolución marginalista: este camino significaba buscar que las probabilidades tuvieran su espacio.
NOTAS AL PIE DE PÁGINA
2. En adelante TPE.
3. En donde se interesaría por los problemas sociales según Black (1976, 1987).
4. Sus trabajos sobre la lógica fueron tan importantes, que fue Cobden Professor of Logical, Mental and Moral Philosophy en Owen College, en 1866.
5. Esta máquina se describe en el "Proceeding of the Royal Society, 20 January 1870". Las bases de esta máquina están en la obra "Sustitución de similares, 1869", de Jevons.
6. En este libro, la lección 21 "Sofismas materiales" es todo un homenaje al libro de De Morgan "Lógica formal".
7. Mirowski usa esta frase para hacer de la energética el núcleo de la obra de Jevons. Esta interpretación es cuestionable en tanto a Jevons debe considerársele a partir de un enfoque meteorológico en torno al método usado en economía según Keynes y, como señalara Salazar (1995) esto "lo distancia y lo coloca en un lugar aparte de su compañero de revolución marginal, Leon Walras" Salazar (pág. 44).
8. El principio de exclusión de términos.
9. Jevons en White (1989).
10. Y no el grado promedio, ya que es en la unidad marginal del bien donde se determina el grado de saciedad del mismo. ¿Por qué no es posible utilizar la utilidad promedio? Debido a que el intercambio sólo se define a partir del grado de utilidad que se pueda derivar de una determinada cantidad de un bien y, una vez determinado el nivel en el cual se sitúa la cantidad necesaria de éste, la utilidad promedio estaría conteniendo la cantidad del bien que no se intercambia en el mercado.
11. Incluyendo la operación inversa del cálculo diferencial: la integral.
12. Un punto de partida problemático, ya que para Jevons "El coste de producción determina la oferta de la utilidad, La oferta determina el grado final de la utilidad, El grado final de la utilidad determina el valor" (Marshall). En primer lugar, esto no parece consistente con la proposición básica según la cual el valor depende solamente del grado final de utilidad, de hecho según las premisas establecidas por Jevons, el primer determinante es el costo clásico de producción, y en segundo lugar "los determinantes del valor hay que buscarlos, en todo caso, no en condiciones causales unilaterales, sino en la determinación recíproca y en la interdependencia" Marshall en Hutchinson (1974, 328).
13. Bob Logan se refiere a la carta que Westergaard le envió a Jevons en 1874, donde se menciona la solución, para encontrar un máximo utiizando el método de Lagrange.
14. Publicada por Black R.D., ver Logan y Yeung (1990).
15. "Theory of political economy 1871 pág. XII".
16. Como puede observarse en la página 84 de la TPE Jevons dice que "El valor de uso de Adam Smith o la utilidad total, es la integral de U.dM y tiene dimensión MV".
17. Jevons pensó que era suficiente con el análisis realizado en el capítulo tercero para definir la utilidad expresable en el mercado, contrario a lo que pensaba Westergaard: Maximizar con restricciones y encontrar las condiciones de primer y segundo orden.
18. El ambiguo concepto de "trading body" es un procedimiento ilícito sobre su propia visión de que las utilidades de diferentes individuos no son comparables. Stigler pág. 91.
19. Walras en Logan (1989).
20. "Así nosotros llegamos al principio que los grados de utilidad de las mercancías intercambiadas podrán estar en proporción inversa de las magnitudes de los incrementos intercambiados" (TPE, pág. 99). Recordemos que el grado de utilidad es definido como "lo estimado o la urgencia de desear más" (TPE, pág. 84) apelando de esta forma a los sentimientos.
21. "La tasa de intercambio de dos mercancías debe ser recíproca a la tasa de los grados finales de la utilidad de las cantidades de una mercancía disponible para el consumo después de que el intercambio es realizado" (TPE, pág. 95).
22. Como opina Blaug: "El grado final de utilidad de Jevons es nuestra utilidad marginal dividida por el incremento marginal. Los libros de texto actuales aún hablan en ocasiones de la utilidad marginal, como si se tratara de la utilidad de la unidad marginal, esto puede dar lugar a errores, la utilidad marginal de la última unidad es la utilidad de cada unidad, puesto que cualquiera de ellas puede ser la última; así podrá obtener la utilidad total multiplicando la utilidad marginal por el número de unidades consumidas" [Blaug(1985) pág. 426] lo cual da lugar a la paradoja de Wieser.
BIBLIOGRAFIA
BLACK, R.D.C. The papers and correspondence of William Stanley Jevons: A supplementary note, Manchester School of Economics and Social Studies, vol. 50(4), Dec, pp. 417-28. 1982.
BLACK, R.D.C. W. S. Jevons and the foundation of modern economics. History of political economy, Manchester School of Economics and Social Studies, Fall, pp. 364-78. 1972
BLACK, R.D.C., COATS, A.W, GOODWING, R.M and CRAWFORD, D.W. The marginal revolution in economics: interpretation and evaluation, Durham, N.C.: Duke University Press. 1979.
BLAUG, M. Economic Theory in retrospect, Fourth Edition, Cambridge: Cambridge University Press. 1985.
BOOLE, G. (1852). Calculus on finite differences, Dover Publications Inc. José Antonio Hernández. Traducción al español Investigación sobre las leyes del pensamiento, Paraninfo, Madrid (1982).
BOOLE, G. An investigation of the law of thought, New York: Dover Publications. 1854.
CREEDY, J. Jevons´s complex cases in the theory of exchange, Journal of the History of Economic Thought, vol. 14(1), spring, pp. 55-69. 1992.
ELLEN, F.P. W. S. Jevons: economic revolutionary, political utilitarian, Journal of the History Ideas, April-Jun. 1972.
JEVONS, W. S. (1952). Logic, Traducción al español, Editorial Pegaso, Madrid.
JEVONS, W. S. (1866). Brief account of a general mathematical theory of political economy. read at the British association. Journal of the statistical society of London, vol. XXIX, pp. 235-53.
JEVONS, W. S. (1871). The theory of political economy. London and New York: MacMillan & Co. Quinta edición
HUTCHINSON, T.W. The politics and philosophy in Jevons, Manchester School of Economics and Social Studies, vol. 50(4), Dec, pp. 366-78. 1982.
HUTCHINSON, T.W. A review of economics doctrines 1870-1929. Oxford: Oxford University Press. 1953.
INGRAO, B and ISRAELSEN, G. The invisible hand: Equilibrium in the history of Science, S.L: The MIT press. 1990.
KRISTRÖN, B. W.S. Jevons (1888) On option value, Journal of environmental economics and Management, 18, pp. 86-67. 1990.
LOGAN, B and YEUNG, S.N. Westergaard, Jevons and early contributions to constrained optimization, Manchester School of Economics and Social Studies, vol, 58(1), March, pp. 20-31. 1990.
MAYS, W. Jevons, conception of scientific method, The Manchester School, 30, pp. 226-49. 1962.
MIROWSKI, P. More heat than light, S.L: New York Cup. 1989.
ROBERTSON, R.M. Jevons and his precursors, Econometrica, vol. 19, pp. 229-249. 1951.
SALAZAR, B. El efecto Piccard y la construcción de la teoría Walrasiana del equilibrio, Lecturas de Economía, núm. 45, juldic, pp. 127-147. 1996.
SALAZAR, B. Esperando a Mirowski, Boletín Socioeconómico, núm. 29, pp. 34-50, dic. 1995.
SCHUMPETER, J. A. History of economics analysis. Oxford: Oxford University Press. 1954.
STIGLER, G. Essays in the history of economics. Chicago: University of Chicago Press. 1965.
STIGLER, G. (1956). Essays in the history of economics: the development utility theory. Chicago: Univ. Chicago Press.
WHITE, M. Why are there no supply and demand curves in Jevons, History of Political Economy, vol. 21(3), Fall, pp. 425-56. 1989.
WOOD, J. C. William Stanley Jevons: Critical assessments. VL I. London and New York: Routledge. 1988.